FRFCM笔记

Cavalier

2025-05-14

#FRFCM #图像分割 #FCM #图像算法

Fast and Robust Fuzzy C-Means Clustering Algorithm Based on Morphological Reconstruction and Membership Flitering - FRFCM

FCM：保留更多原始图像信息。但是由于只考虑灰度信息而不考虑空间信息，对于纹理和背景复杂的图像或被噪声破坏的图像，无法进行分割。

FCM_S，FCM_S1，FCM_S2：允许一个像素点的标签影响其周围像素点的标签，然而每一次迭代都需要计算空间邻居项，所以FCM_S十分耗时。S_1与S_2则在其基础上通过均值滤波与中值滤波提前获取空间邻域信息。降低了计算复杂度。然而FCM_S1，FCM_S2对于噪声都不具有鲁棒性，并且在使用这两种算法时，很难提前获取噪声的类型与强度，从而做出滤波的选择。

EnFCM：基于灰度直方图而不是汇总图像的像素点进行聚类，计算时间很低，但是分割结果不好。

FGFCM：为改善EnFCM，引入一个新的因子作为局部相似性的度量，旨在保证图像分割时的抗噪性和细节保持性，同时去掉EnFCM中需要经验设定的参数，最后仍然是对灰度直方图进行聚类。虽然FGFCM具有更好的鲁棒性但是需要更多的参数设定。

FLICM：将FGFCM中的参数替换为新的模糊因子G_{ki}，并将其纳入目标函数，以保证图像的抗噪性和细节保持性。虽然FLICM克服了参数选择的问题，但是固定的空间距离对不同的图像局部信息不具有鲁棒性

RFLICM：利用可变的局部系数代替固定的空间距离，可以在图像中利用更多的局部上下文信息。

KWFLICM：在FLICM基础上引入核度量，采用加权模糊因子自适应控制局部空间关系。实际使用中，参数的选择取决于图像块与图像的局部统计信息。

NWFCM：图像块已经成功用于非局部去噪和纹理特征提取，基于图像块的相似度度量可以获得更高的分类精度。因此通过图像块的特征自适应选取参数，将非局部空间信息引入到目标函数中，从而克服参数选择的问题，改善对噪声的鲁棒性。然而基于图像块的非局部滤波和参数估计有很高的计算复杂度。为了减少FLICM和KWFLICM的计算时间，通过图像块的距离得到的邻域加权距离代替FCM目标函数中的欧式距离。效果上比FLICM与KWFLICM更快，但是图像块距离和参数选择仍然耗时较长。

NDFCM：基于噪声检测的自适应FCM算法，通过灰度级的局部方差自动调整权衡参数，尽管NDFCM使用了很多的参数，但是它的速度很快，因为图像滤波操作是在迭代开始之前进行的。

FRFCM：基于形态学重构和隶属度滤波的快速鲁棒模糊C均值聚类算法。

提出的FRFCM利用形态学重构对图像进行平滑处理，提高图像的抗噪声能力。同时保持图像额细节信息，解决了现有的算法中需要针对不同的噪声类型选取不同的滤波器的困难。

提出的FRFCM改进了隶属度划分方式，采用了更快的隶属度滤波，去代了局部空间紧邻像素与其聚类中心之间较慢的距离计算，从而降低计算复杂度。

为什么使用形态学重构

FCM改进算法的目标函数一般情况如下所示：

J_m = \sum_{i=1}^{N}\sum_{k=1}^{c}u_{ki}^m\parallel x_i-v_k\parallel^2+\sum_{i=1}^{N}\sum_{k=1}^{c}G_{ki}

不同的改进也就是使用不同的G_{ki}，不同的G_{ki}决定了不同算法的计算复杂度。

在实际使用中，我们希望对与不同的噪声类型污染的图像都能获得一个效果最好的\hat{x_i}在移除噪声的同时能够保留图像中的细节。基于形态学重构的处理就是获取更好的\hat{x_i}。MR利用标记图像重建原始图像，从而获得更好的图像效果。

为什么使用隶属度滤波

在传统的FCM算法中，更新隶属度矩阵与计算聚类中心的方法如下：

u_{ki} = \frac{1}{\sum_{j=1}^{c}(\frac{\parallel x_i-v_k\parallel^2}{\parallel x_i-v_j\parallel^2})^{\frac{1}{m-1}}}

v_k = \frac{\sum_{i=1}^{N}u_{ki}^{m}\cdot x_i}{\sum_{i=1}^{N}u_{ki}^{m}}

而FLICM与KWFLICM的隶属度更新公式中，如下所示：

u_{ki} = \frac{1}{\sum_{j=1}^{c}(\frac{||x_i-v_k||^2+G_{ki}}{||x_i-v_j||^2+G_{ji}})^{\frac{1}{m-1}}}

因为G_{ki}无法预先计算，所以会使得迭代过程中的计算量大，计算复杂度高。

在FRFCM中，将隶属度滤波引入到FCM中以解决上述的矛盾。因为形态学重构是预先计算的，对重构图像的灰度直方图进行聚类。在获取到模糊隶属度矩阵U_{ki}后，采用隶属度滤波对隶属度矩阵进行修正，免去了局部空间近邻像素点与聚类中心点的距离运算。

FRFCM方法概览

与EnFCM相似，提出的FRFCM的聚类是在灰度直方图上进行的，因此目标函数可以写成：

J_m = \sum_{l=1}^{q}\sum_{k=1}^{c}\gamma_l u_{kl}^m\parallel\xi_l-v_k\parallel^2

u_{kl}表示灰度级l对簇类k的隶属度。并且有如下关系：

\sum_{l=1}^{q}\gamma_l = N

\xi是经过形态学重构之后的图像，并且\xi_l是一个灰度级。其中1\le l\le q，q为形态学重构图像中包含灰度级的数量，通常情况q远小于N。

当形态学重构图像中的灰度级很多的时候，会不会使算法对图像的分割效果出现下滑，如何解决？

\xi = R^C(f)

其中R^C表示形态学闭合重建，f表示原始图像。

通过拉格朗日乘子法，上述的优化问题可以转化为一个非约束优化问题，是如下目标函数最小化即可：

\widetilde{J_m} = \sum_{l=1}^{q}\sum_{k=1}^{c}\gamma_l u_{kl}^m\parallel \xi_l-v_k\parallel^2-\lambda(\sum_{k=1}^{c}u_{kl}-1)

\lambda是拉格朗日乘子。使得目标函数\widetilde{J_m}最小就是找到目标函数的鞍点，分别关于u_{ki}和v_k对其求导，得到u_{ki}和v_k的值满足如下：

u_{kl}= \frac{\parallel\xi_l-v_k\parallel^{-\frac{2}{m-1}}}{\sum_{j=1}^{c}\parallel\xi_l-v_j\parallel^{-\frac{2}{m-1}}}

v_k = \frac{\sum_{i=1}^{q}\gamma_l u_{kl}^m\xi_l}{\sum_{i=1}^{q}\gamma_l u_{kl}^m}

根据公式（9），通过初始化获得的隶属度划分矩阵U= [u_{kl}]^{c\times q}，为获取稳定的隶属度划分矩阵，通过重复进行公示（9）与公示（10）的迭代，直到\max{\{U^{(t)}-U^{(t+1)}\}}<\eta。其中\eta是设定的最小误差阈值。

因为u_{kl}^{(t)}表示的是灰度级l对于簇类k的隶属度，对于一个新的隶属度划分矩阵U' = [u_{kl}]^{(c\times N)}，他对应于原始图像f来获得：

u_{ki} = u_{kl}^{(t)}，\text{if}\quad x_i = \xi_l

为了得到更好的隶属度划分矩阵，加快算法的收敛速度，我们使用隶属度滤波对算法进行改进。考虑到隶属度滤波性能和算法速度之间的折中，本文采用中值滤波：

U'' = \text{med}\{U'\}

基于上述分析，提出如下算法过程：

设置聚类的簇类数量c，模糊加权指数m，滤波窗口大小w和最小误差阈值\eta
通过公式（7）计算形态学重构后的图像\xi，与重构后图像\xi的直方图
初始化隶属度矩阵U^{(0)}
设置循环计数器t=0
使用公式（10）更新聚类中心点。
使用公式（9）更新隶属度划分矩阵U^{(t+1)}
判断隶属度矩阵的变化误差是否小于\eta，是则停止，否则将t=t+1，转到步骤5
使用提前确定的滤波对隶属度划分矩阵进行处理

形态学重构

对于FCM算法来说，其收敛速度总是由数据的分布特征来决定的，如果数据的分布特征有利于聚类，那么对应的迭代次数就会比较少，反之，迭代次数就会比较多。FCM对噪声很敏感，因为数据的分布特征总是会受到噪声破坏的影响，这样会导致两个问题。

FCM算法对含噪声的图像的分割效果较差。
FCM算法对受噪声污染的图像的迭代次数大于未受噪声污染的图像。

众所周知的是，数据的分布特征可以用直方图来描述。如果图像的直方图是均匀的那就很难实现良好的，快速的图像分割。相反的，如果图像的直方图有多个显著的峰值，那么就会很容易得到好的图像分割效果。

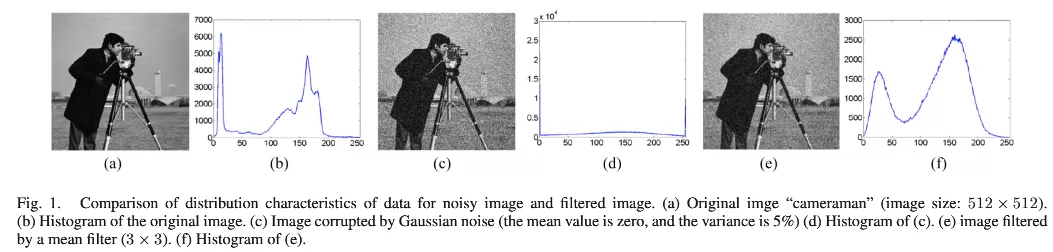
如上图所示，在高斯噪声的影响下，其灰度直方图没有明显的峰值，但是在通过均值滤波进行处理之后，其直方图出现了明显的峰值，可以说明均值滤波对于优化数据分布是有效的。

这里主要论证的是均值滤波对于优化图像中像素点灰度值数据的分布是有效的。而不是说均值滤波对于噪声是有效的。

如果通过一种滤波可以优化图像数据的分布，那么就可以获得效果更好的图像分割效果。

根据实际场景，如果需要的分割效果是那种精确的，那么就可以根据场景中的特点选择优化分布的方法。

本文将形态学重构算法引入到FCM算法中，在聚类之前对数据的分布特性进行优化。形态学重构能在不知道图像中噪声类型的前提下保持目标轮廓并移除噪声，有利于优化数据的分布特性。形态学重构有两种基本的方式，分别为：形态膨胀重建与形态腐蚀重建。膨胀重建使用R_{f}^{\delta}(g)表示，定义为：

R_{f}^{\delta}(g)=\delta_f^{(i)}(g)

其中f为原始图像，g是标记图像，且g\le f，\delta是膨胀算子。

\delta_f^{(1)}(g)=\delta(g)\land f\quad;\quad \delta_g^{(i)}(f) = \delta(\delta^{(i-1)}(g))\land f

其中\land表示逐对计算最小值。

由对偶性，形态学腐蚀重构表示为R_f^{\varepsilon}(g)，定义为：

R_{f}^{\epsilon}(g) = \varepsilon_f^{(i)}(g)

其中g\ge f，\varepsilon是腐蚀算子

\varepsilon_f^{(1)}(g) = \varepsilon(g)\lor f \quad;\quad \varepsilon_{g}^{(i)}(f) = \varepsilon(\varepsilon^{(i-1)}(g))\lor f

其中\lor表示逐对计算最大值。

对于聚醚砜滤膜的上层滤孔的分割，因为会有滤孔叠加的情况，使得上层气孔在常规的FRFCM中无法正确分割。

FRFCM为什么适合用于滤孔的分割。

FRFCM迭代聚类速度快。

FRFCM基于形态学重构可以有效地消除微小滤孔的影响。

但是传统的FRFCM对于滤孔叠加的问题无法解决。会出现错误分割的情况。在聚类的过程中通过分割的连通域效果进行形态学重构影响因子的影响程度增强，以解决滤孔叠加导致错误分割的情况。

图像的形态学重构结果取决于标记图像和掩码图像的选择。一般情况下，如果将原图像作为掩码图像使用，则将原图像的变换视为标记图像。

在实际应用中，g=\varepsilon(f)用于膨胀重构(g\le f)，g=\delta(f)用于腐蚀重构(g\ge f)，以获得一个标记图像。

在膨胀重构与腐蚀重构的基础上，可以得到一些滤波能离较强的重构算子，比如形态学中的开闭运算重构。由于用R^C表示的闭运算重构更适用于纹理细节平滑。我们用它修改原始图像，它的定义如下所示：

R^C(f) = R^\epsilon_{R^{\delta}_{f}(\varepsilon(f))}(\delta(R^{\delta}_{f}(\varepsilon(f))))

在“MR brain image segmentation using an enhanced fuzzy c-means algorithm”中，修改的图像\xi = (\xi)_{i=1}^{N}定义为：

\xi_i = \frac{1}{1+\alpha}(x_i + \alpha\hat{x}_i)

在上式（18）中，x_i\in f,x_i'\in R^C(f)。为了获取标记图像，对于\delta或\varepsilon，需要一个包含中心元素的结构单元B。如：\varepsilon_B(f)\le f且\delta_B(f)\ge f，则可以将R^C重写为：

R^C(f) = R^{\varepsilon}_{R^{\delta}_{f}(\varepsilon_B(f))}(\delta_B(R^{\delta}_{f}(\varepsilon_B(f))))

形态学重构的想法用于FCM中，核心就是通过形态学重构来消除噪声影响，而且因为形态学重构运算迅速，并且可以在迭代聚类之前就获取形态学重构之后的标记图像。那么形态学重构所得的信息在聚类过程中是如何体现并且影响聚类结果的。

隶属度滤波

根据上述内容，我们发现引入局部空间信息对于改建FCM算法是有用和有效的。然而，局部空间近邻和聚类中心内像素间距离的计算具有较高的复杂度。在FLICM中如果移除G_{ki}，那么FLICM与FCM就是相同的了。为此，通过一种简单的方式替换G_{ki}，其中不需要计算局部空间邻域内的像素和v_k之间的距离。

在这一思想的启发下，引入了隶属度滤波。使用隶属度比例的空间邻域信息替换G_{ki}的贡献。

在FLICM与KWFLICM中，u_{ki}依赖于两个距离的计算：x_i，x_j分别到v_k的距离。但是x_j到v_k的距离计算是重复且冗余的，因为只要计算了x_i到v_k的距离，就可以以此获取x_j到v_k的距离。综上，可以通过隶属度滤波器来纠正错误分类的像素，即不需要计算像素的近邻与聚类中心点之间的距离，根据原有的G_{ki}，修改后的隶属度划分为：

u'_{ki} = u_{ki}+ \sum_{j\in N_i;i\ne j}\frac{1}{d_{ij}+1}u_{kj}

形态学重建

形态学重建涉及两幅图像和一个结构元：一幅图像是标记，使用F来表示，它包含重建的起点；另一幅图像是模板，使用G来表示，模板用于约束重建。结构元用于定义连通性，连通性默认使用8连通。

在形态学重建中，重点就是选取标记点，也就是根据图像特征选取想要的纹理特征中的标记点。在膨胀中，标记点膨胀为区域，根据这个区域与模板图像的交集获取标记点附近的纹理特征。

在选取纹理特征时依据原图像可能无法获取完整的纹理特征，那么根据形态学重建，可以达到一个更好的效果。

传统的形态学处理是选取一个结构元，自定义核，之后对整个图像进行形态学处理。这样的效果就是不可控的。在形态学重建中，是只针对一部分特征点进行形态学处理，并且处理之后的结果需要以模板图像为限制。

二值图像形态学重建

测地膨胀与测地腐蚀

形态学重建的核心就是测地膨胀与测地腐蚀的概念。令F表示标记图像，G表示模板图像。这里假设两个图像都是二值图像，且F\in G。标记图像相对于模板大小为1的测地膨胀定义为：

D_{G}^{(1)} = (F\oplus B)\cap G

F相对于G的大小为n的测地膨胀定义为：

D_{G}^{(n)} = D_{G}^{(1)}[D_{G}^{(n-1)}(F)]

式中，n\ge 1是整数，D^{(0)}=F。在这个递归公式中，每一步都是膨胀后取交集。交集运算可以保证模板G限制标记F的生长（膨胀或腐蚀等形态学运算）。下图是大小为1的测地膨胀。

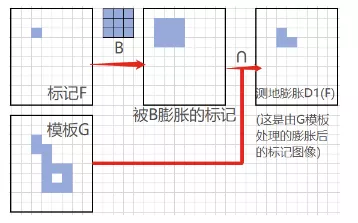
标记F相对于模板G的大小为1的测地腐蚀定义为：

E_{G}^{(1)} = (F\ominus B)\cup G

标记F相对于模板G的大小为n的测地腐蚀定义为：

E_{G}^{(1)} = E_{G}^{(1)}[E_{G}^{(n-1)}(F)]

上式中，n\ge 1是整数，E^{(0)}=F。在这个递归公式中，每一步都是腐蚀后取并集，以保证图像的测地腐蚀仍然大于模板图像。下图为大小为1的测地腐蚀示意图：

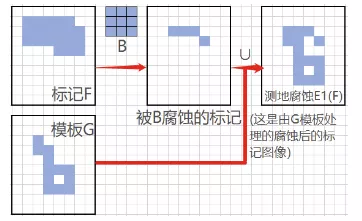
简单来说，测地膨胀和测地腐蚀就是有条件的膨胀和腐蚀。膨胀或腐蚀的结果与模板图像进行交集或并集运算，从而对膨胀或腐蚀操作施加了特定的约束。

腐蚀和膨胀的形态学重建

根据上述测地腐蚀与测地膨胀的概念，标记图像F相对于模板图像G的膨胀形态学重建，定义为：

==F相对于G的测地膨胀，反复迭代至稳定状态为止==

相对于膨胀重建，腐蚀重建与之同理。

示例：重建开运算

在形态学开运算中，腐蚀会删除小目标，而膨胀会试图恢复保留的目标的形状。恢复的精度取决于目标的形状和所用结构元的相似性。重建开运算能够精确地恢复腐蚀后所保留目标的形状。图像F的大小为n的重建开运算定义为，F的大小为n的腐蚀相对于F的膨胀重建，即：

O_{R}^{(n)}(F) = R_{F}^{D}(F\ominus nB)

重建开运算采用F的腐蚀结果作为膨胀重建的标记。

灰度级形态学重建

灰度级的测地膨胀与测地腐蚀

假设f和g是相同大小的灰度图像，且f\le g，即f在图像中任一点的灰度比g在这一点的灰度小。f相对于g的大小为1的测地膨胀定义为：

D_{g}^{(1)}(f) = (f\oplus b)\land g

其中\land表示逐点最小算子，b是一个合适的结构元。根据上式可以看出，大小为1的测地膨胀的获得方式如下：首先计算b对f的膨胀，然后选择(x,y)处膨胀结果和g之间的最小者。f相对于g的大小为n的测地膨胀为：

D_{g}^{(n)}(f) = D_{g}^{(1)}[D_{g}^{(n-1)}(f)]

类似的，f相当于g的大小为1的测地腐蚀定义为：

E_{g}^{(1)}(f) = (f\ominus b)\lor g

其中\lor表示逐点最大算子。f相对于g的大小为n的测地腐蚀定义为：

E_{g}^{(n)}(f) = E_{g}^{(1)}[E_{g}^{(n-1)}(f)]

灰度图像重建开运算：

O_R^{(n)}(f) = R_{f}^D(f\ominus nb)

先腐蚀输入图像，然后将腐蚀后的图像作为标记图像，将图像本身作为模板，进行膨胀，反复迭代至稳定。

重建闭运算：

C_{R}^{(n)}(f)=R_{f}^{E}(f\oplus nb)

先膨胀再腐蚀，最后求图像的补集。