变分水平集图像分割方法

#图像分割
30

变分水平集图像分割方法

A Level Set Model for Image Classification

Abstract

提出了一个基于变分方法的监督分类模型。该模型致力于寻找由具有规则借口的同构类组成的最优划分。所提出的方法的独创性涉及通过使用水平集来定义分区。与类关联的每组区域和边界由唯一的水平集函数定义。我们使用与不同类别一样多的水平集，并且由于相互作用的能量，所有这些水平集都在同时移动以获得图像的最佳分区。我们通过最小化唯一函数来定义这些力。通过动力学方案考虑与泛函最小化相关的耦合偏微分方程。给定一个初始界面集即零水平集，偏微分方程的不同项控制着界面的运动，因此在收敛时，我们得到一个如上所述的最佳划分。每个界面都由内部力量（界面的规律性）和外部力量（数据项，无真空，无重叠区域）引导。

Introduction

分类问题与分割问题密切相关，因为我们想要的到由同质区域组成的分区。然而，在分类过程中，每个分区代表一个类，即一组具有相同标签的像素。在本文中，我们感兴趣的特征标准时空间分布强度（或是灰度级）。所提出的方法同时可以扩展到灰度级以外的其它判别特征，如，纹理。

例如，如果我们假设类别的数量和统计数据由估计算法给出，则问题是针对这些类别定义图像的分区，以便每个像素代表指定的类的同时定义了具有规则边界的同质区域。监督分类的难度取决于这种折中的实现。

变分方法和偏微分方程模型已经被证明可以有效解决各种图像处理问题，例如恢复和边缘检测。在分割方法中，区域的数量和相关的边界集是未知的，目标是获得具有规则边界的同质区域。分类的概念，包括为图像的每个位置分配一个标签，很少在变分公式（连续模型）中引入，主要是因为类的概念具有离散的性质。即使估计了类的数量和统计数据，我们不知道形成每个类别的区域数量。至于分割，我们正在寻找一个正则化的分区，但标记过程导致定义一个耦合力惩罚错误分类和未分类的像素。许多分类模型都是用结构概念开发的，如区域生长法或是通过随机方法使用马尔可夫随机场理论，随机方法是鲁棒但是十分耗时的。

为了同时对区域和边界进行建模，Samson等人提出了第一个模型

Samson模型

Samson模型介绍

设图像区域​\Omega\in \R^2，灰度图像​f(x):\Omega\to \R。Samson等认为图像聚类就是寻找一个开集合组​\{\Omega_i\}_{i=1}^{k}满足下列条件：

  1. ​\{\Omega_i\}_{i=1}^{k}是图像区域​\Omega的一个划分，即​\Omega = \cup_{i=1}^{k}(\Omega_i\cup\Gamma_i),\Omega_i\cap\Omega_j = \varnothing,i\ne j，其中​\Gamma_i表示​\Omega_i的边界，定义为​\Gamma_i = \partial\Omega_i\cap\Omega。
  2. 对于​f(x),x\in\Omega_i,\forall i =1,\cdots,k，服从期望为​c_i、方差为​\sigma_i的Gauss分布。
  3. 聚类边界的正则化，即相邻聚类的边界​\Gamma_{i,j} = \Gamma_i\cap\Gamma_j。

Samson采用水平集理论，成功将变分法应用到图像聚类中，设水平集函数​\phi_i(x):\Omega\to\R满足以下条件：

\begin{cases} \begin{aligned} &\phi_i(x)>0,\quad x\in\Omega_i\\ &\phi_i(x) = 0,\quad x\in\Gamma_i\\ &\phi_i(x)<0,\quad x\in\frac{\Omega}{\Omega_i\cup\Gamma_i} \end{aligned} \end{cases}

那么就将上述1~3的聚类问题转换为求解以下极小值的问题：

\begin{aligned} \inf_{\phi_i}\{&\sum_{i=1}^{k}e_i\int_{\Omega}\frac{(f(x)-c_i)^2}{\sigma_i}H(\phi_i(x))dx+\\ &\sum_{i=1}^{k}\gamma_i\int_{\Omega}g(f(x))|\triangledown H(\phi_i(x))|dx+\\ &\frac{1}{2}\kappa\int_{\omega}(\sum_{i=1}^{k}H(\phi_i(x))-1)^2dx\} \end{aligned}

可以将上式理解为一个多方面的能量，其中第一项是聚类能量，其主要作用是将图像​f(x)聚类为​k个均值为​c_i、方差为​\sigma_i的Gauss分布的同质区域；第二项是正则化能量，使得聚类边界长度尽可能的小和光滑；第三项是惩罚能量，其主要作用是惩罚过聚类和空聚类，过聚类就是像素点同时被聚类到多个聚类区域，空聚类就是像素点没有被任何一个聚类区域包含。

Samson模型的不足

  1. 此模型实际上是K-means聚类。
  2. 聚类能量基于图像的全局信息，使得聚类结果对噪声过于敏感。

基于区域信息的水平集模型理论

基于区域信息的活动轮廓模型思想是将基于图像灰度信息的能量项添加到能量方程中，去除基于梯度信息的能量项，并使用灰度或纹理差异分割目标对象。最为经典的是变分水平集方法，该模型被称为C-V模型，与传统的水平集方法相比，该方法更加方便、更自然地加入了基于区域的信息和形状先验信息作为附加约束，从而使模型初始化更灵活和更大的收敛范围。

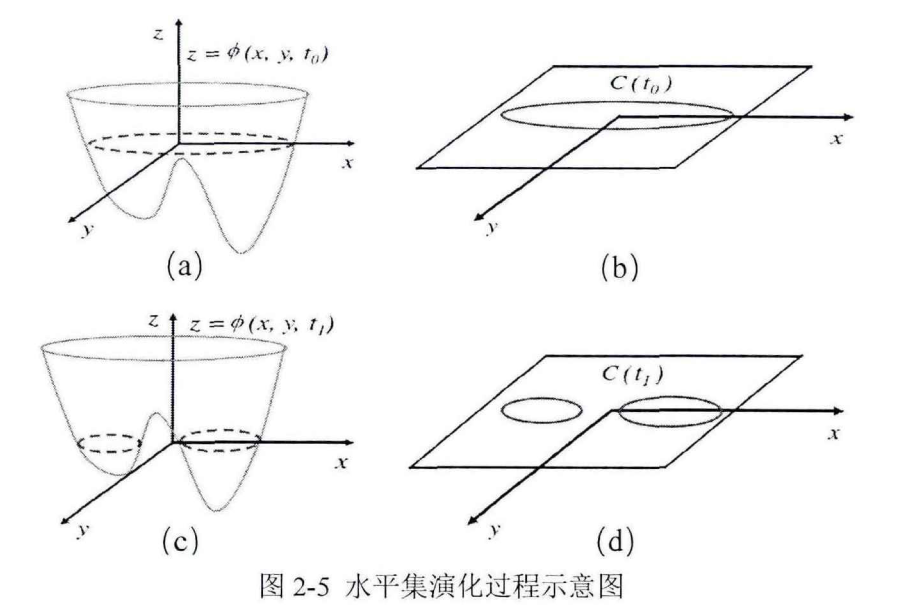
image-20221207113846668

基于传统水平集函数首先设定一个初始轮廓曲线​C_i，然后通过泛函能量最小化原理对​C_i进行演化，此时该函数可定义为：

Q = u(x,y,t)
u(x,y,t) = 0

上式中：​u(x,y,t)表示水平集函数​Q的零点水平位置，上图中(a)和(c)分别表示​Q = u(x,y,t)在​t_0和​t_1时刻的零水平集位置。

水平集方程可通过函数​Q演化获得：

\frac{\partial u}{\partial t} = F|\triangle u| = 0

上式中：​F表示曲线​C_{t}的速度函数。

\frac{\partial u}{\partial t} = \delta(u)[vdiv(\frac{\triangledown u}{|\triangledown u|})+(-\lambda_1)(I_0(x,y)-C_a)^2+\lambda_2(I_o(x,y)-C_b)^2]

上式中：​v,\lambda_1,\lambda_2分别表示能量项的权重系数，​I_0(x,y)表示图像中​(x,y)位置像素点的灰度值，​C_a表示曲线内部区域的灰度均值，​C_b表示曲线外部区域的灰度均值。

Heaviside和Dirac函数为：

H_{(p)} = \begin{cases}1\qquad p>0\\0\qquad p<0\end{cases}
\delta_{(p)} = \frac{d}{dp}H_{(p)}

算法流程如下：

  1. 定义初始水平集函数​u_0(x,y)为：
u_0(x,y) = \begin{cases} \begin{aligned} -\rho\qquad&(x,y)\in\Omega_0\\ 0\qquad&(x,y)\in C_{(t)}\\ \rho\qquad&(x,y)\in \Omega_1 \end{aligned} \end{cases}

式中：​\rho>0为常数，​(\Omega_0,C_{(t)},\Omega_1)\in\Omega，​\Omega为整个图像，该函数的梯度满足​|\triangledown\phi| = 1。

  1. 设定速度函数​F的表达式来决定演化的形式。
  2. 求解在不同时间状态下的零水平集位置。

针对于C-V模型，该模型的能量函数可以定义为：

F_{(C_1,C_2,C_3)} = \mu\times Lenth(C)+v\times Area(inside(C))+\lambda_1

式中：​I表示原图像，​C表示轮廓曲线，​Lenth(C)表示该轮廓曲线的长度，​Area(inside(C))表示该轮廓缺陷所构成的面积，​\mu,v>0分别表示各能量对应的权重系数；​I_o(x,y)表示像素灰度值。

用水平集函数表示C-V模型的能量泛函：

F(c_1,c_2,\phi)=\mu L(c_1)+vS_0(c_1)+\lambda_0\int\int_{\Omega_0}|I-c_2|^2dxdy+\lambda_0\int\int_{\Omega_1}|I-\phi|^2dxdy

式中：​c_1表示活动轮廓曲线，​E = \mu L(c_1)+vS_0(c_1)表示内部能量项，有平滑曲线的作用。​L(c_1)表示轮廓曲线的长度；​S_0(c_1)=\int\int_{\Omega_0}dady表示闭合曲线内部区域的面积；其中​\mu,v>0切均为常数。​c_2,\phi分别表示最终分割轮廓线的位置以及未知数。