Matrix Profile I-时间序列的全对相似性连接

#Matrix Profile #时间序列
16

Introduction And Background

全对相似性连接问题有很多种变体，其基本任务为：给定一组数据对象，检索每个对象的最近邻居。与​K近邻相似，对于时间序列，如果需要检测子序列的前​K个最近邻或每个对象的最近邻（如果在近邻子序列在阈值​\tau内）。

这种对于阈值​\tau的依赖在时间序列更加关键：

  1. 与相似度不同（在零到一之间有界），欧式距离实际上是一个无界的数值，而且通常来讲不直观。
  2. 对于非常相似的数据集，单个阈值也会产生截然不同的输出大小。

Definition

Definition 1:

时间序列​T是实数值序列​t_i :T=t_1,t_2,\dots,t_n，其中​n是时间序列​T的长度。

Definition 2:

时间序列​T的子序列​T_{i,m}是从位置​i开始的长度为​m的连续子集。

T_{i,m} = t_i,t_{i+1},\dots,t_{i+m-1},1\le i\le n-m+1

Definition 3:

距离分布​D是一个用于查询所有子序列集中每两个子序列之间的欧式距离的向量。在Matrix Profile中子序列之间的距离由​z-normalized子序列之间的欧几里得距离进行测量。

Definition 4:

时间序列​T的全子序列集合​A是通过在时间序列​T上滑动长度为​m的窗口获得的​T的所有可能子序列的有序集合：

A = \{T_{1,m},T_{2,m},\dots,T_{n-m+1,m}\}

其中​m是用户定义的子序列长度。通过​A[i]来表示​T_{i,m}。

Definition 5:

​1NN-join函数：给定两个全子序列集​A和​B以及两个子序列​A[i]和​B[j]，一个​1NN-join函数​\theta_{1nn}(A[i],B[j])是一个布尔函数，当且仅当​B[j]是集合​B中的子序列​A[i]的最近邻子序列时会返回“true”。

使用定义的连接函数，可以通过在两个输入全子序列集上应用相似性连接运算符来生成相似性连接集。

Definition 6:

相似性连接集：给定所有子序列集​A和​B，​A与​B的相似性连接集​J_{AB}是包含​A中每个子序列与其在​B中最近邻配对的集合，形式化地表示为​J_{AB} = A_{\bowtie\theta_{1n}}B。

测量相似性连接集中每对之间的欧氏距离，并将结果存储到一个有序向量中，称该结果向量为矩阵轮廓。

Definition 7:

矩阵轮廓（简称轮廓）​P_{AB}是一个向量，包含​J_{AB}中每对之间的欧氏距离。

我们称这个向量为矩阵轮廓，因为计算它的一种方法是计算一个时间序列中所有子序列与另一个时间序列中所有子序列的完整矩阵距离，并提取每一行中的最小值（自连接情况下为最小的非对角线值）。如下图所示：

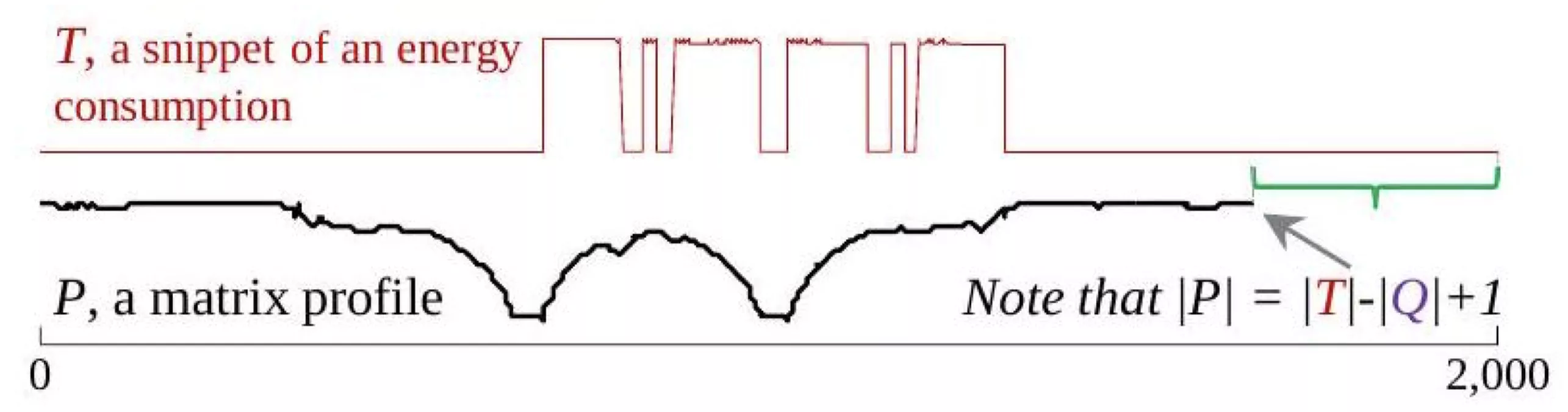
image-20250509113140929

类似于距离轮廓，矩阵轮廓可以被视为一个元时间序列，用于注释时间序列​T，如果矩阵轮廓是通过将​T与自身连接生成的。该轮廓具有许多有趣且可利用的特性，例如，轮廓上的最高点对应时间序列异常点，最低点对应最佳时间序列模式对的位置，方差可以看作是​T复杂度的度量，此外，矩阵轮廓中数值的直方图正是时间序列密度估计的结果。

将相似性连接集合（Definition 6）的这个特殊情况明明为自相似性连接集合，并将相应的概要称为自相似性连接概要。

Definition 8:

自相似性连接集合​J_{AA}是集合​A与其自身进行相似性连接的结果，我们正式表示为​J_{AA} = A_{\bowtie_{\theta 1nn}}A。我们将相应的矩阵概要或自相似性连接概要表示为​P_{AA}。

注意，当执行自相似性连接时，我们排除平凡匹配，即如果​A[i]和​A[j]是来自同一全子序列集合​A,\theta_{1nn}(A[i],B[j])的子序列，当​A[i]和​A[j]是一堆普通匹配时，​A,\theta_{1nn}(A[i],B[j])为"false"。

矩阵概要中的​i^{th}元素告诉我们从​T的子序列开始于​i的最近邻的欧氏距离。然而，它并不告诉我们该邻居的位置，此信息记录在矩阵概要索引中。

Definition 9:

相似连接集合​J_{AB}的矩阵轮廓索引​I_{AB}是一个整数向量，如果​\{A[i],B[j]\}\in J_{AB}其中​I_{AB}[i]=j

通过以这种方式存储近邻信息，可以通过访问矩阵轮廓索引中的第​i个元素，高效地检索​A[i]的最近邻。

Algorithms

1. Mueen's ultra-fast Algorithm for Similarity Search(MASS)

首先介绍一种用于时间序列数据的新颖欧氏距离相似性搜索算法，该算法不仅找到查询的最近邻，并且还会返回其距离。

image-20250509134436269

image-20250509135010458