DTW与WDTW动态时间规整

动态时间弯曲距离

在时间序列分析中，时间序列的相似性度量是衡量两条时间序列相似程度的度量方法，是时间序列聚类分析中一个不可缺少的步骤。因此，度量距离的大小决定了时间序列的相似程度，相似性度量方式的特点决定了相似性度量的效果。动态时间弯曲是时间序列相似性度量中常用的方法。

动态时间弯曲距离不仅可以消除欧式距离点对点的匹配缺陷，通过弯曲时间达到时间序列一对多的匹配，实现不等长时间序列的度量，还对时间序列的偏移、振幅变化等情况具有较强的鲁棒性。

目前，针对于动态时间弯曲的主要研究主要分为以下几个方面：

1. 如何提高动态时间弯曲的度量效率
2. ==如何提高动态时间弯曲的度量质量==
3. 动态时间弯曲在各中数据中的应用性能

在给定两条时间序列时​S = \{s_1,s_2,\cdots,s_n\}与​Q=\{q_1,q_2,\cdots,q_m\}，两条时间序列分别表示在本场景中的误判数据时间序列与正确判断的时间序列。

以上述两条时间序列中的任意两点之间的距离确定​n\times m的距离矩阵​D_{n\times m}，其中

​D(i,j)即为点​s_i与​q_i之间的距离，其中​i=1,2,\cdots,n，​j = 1,2,\cdots,m，当​w=2时距离度量方式即为欧式距离。为了计算​S和​Q的动态时间弯曲距离​DTW(S,Q)，需要找到一条最优的弯曲路径​P_{best}=\{p_1,p_2,\cdots,p_K\}\quad max(n,m)\le K \le n+m+1使得​S和​Q的累积距离值达到最小，​p_K表示该弯曲路径元素在距离矩阵中的位置，即​p_K = (i,j)_K表示​s_i与​q_j之间的匹配关系，可知​D(p_K) = D(i,j)_K一般存在着多条弯曲路径，有效的弯曲路径​P必须符合给出的3个要求：

1. 边界性：​p_1=(1,1),p_K=(n,m)
2. 单调性：给定​p_k=(i,j)和​p_{k+1}=(i',j')有​i'\ge i,j'\ge j
3. 连续性：给定​p_K=(i,j)和​p_{k+1}=(i',j')有​i'\le i+1,j'\le j+1

边界性确定了起始点和终止点在左下角与右上角，单调性和连续性保证了弯曲路径的下一个点在当前点的上方，右上方或右方。在众多有效路径中找到唯一的最优路径是的累积距离达到最小，即：

对于DTW的度量效果研究

针对度量效果的改进主要是针对距离矩阵的构建过程、累积代价矩阵的构建过程的改进。

为了更合理的动态时间弯曲度量效果，利用时间序列数据点的相位差提出了WDTW方法，在距离矩阵中相位差越高的元素将被赋予越高的惩罚权重，避免了时间序列过度弯曲和不合理匹配的问题。

DTW更多地考虑时间序列的值特性，而忽略了时间序列的形态特性，并且存在畸形匹配的问题。

加权动态时间弯曲距离（Weighted Dynamic Time Warping- WDTW）

WDTW在采用一种修正的逻辑权重函数度量非线性匹配时，由数据在时间轴上的偏移而造成的重要性差异有效避免畸形匹配的问题。

进而出现，将​K维多元时间序列视为​K维空间的曲线，运用欧式距离作为基距离，并采用微分动态时间弯曲算法计算多元时间序列的相似性，然而该方法将各个变量看成相互独立的维度空间，割裂了各个变量之间的相关性。

WDTW解决了DTW的畸形匹配问题，但仍然忽略了时间序列的形态特征问题。

标准的DTW计算所有点的距离，每个点的惩罚相等，而不考虑相位差。所提出的WDTW根据测试点和参考点之间的相位差对点进行惩罚，以防止异常值引起的最小距离失真。关键思想是，如果相位差低，则施加较小的权重（即惩罚较小），因为相邻点是重要的。如果相位差是较高的则施加较大的权重。

在WDTW算法中，在创建​m\times n路径矩阵时，​s_i和​q_j两点之间的距离计算为​d_w(s_i,q_j)=\parallel w_{|i-j|}(s_i-q_j)\parallel_p，其中​w_{|i-j|}为​s_i与​q_j两点之间的权重值。这意味着当我们计算序列​S中的点​s_i与序列​Q中的点​q_j之间的距离时，权重值将根据相位差​|i-j|确定。换而言之，如果两个点​s_i与​q_j接近，则可以施加较小的权重。因此两个序列之间的最优距离被定义为所有序列的最小路径。

其中​\gamma^*(i,j)=|w_{|i-j|}(s_i-q_j)|^p+\min{\gamma^*(i-1,j-1),\gamma^*(i-1,j),\gamma^*(i,j-1)}

基于对​l_p空间的经典分析，我们提出了如下两个命题以显示WDTW的一些数学性质，如WDTW距离随着​p的增加而单调减小，并且在测量空间上的特定条件下可以得到相反的结果。

命题一：

对于​0<p<q\le\infty，​\text{WDTW}_p(s_i,q_j)\ge\text{WDTW}_q(s_i,q_j)

命题二：

对于​0<p<q\le\infty，​\text{WDTW}_p(s_i,q_j)\le(2n-2)^{(1/p)-(1/q)}\text{WDTW}_q(s_i,q_j)，==其中​n是两个序列的长度==

给定两个序列的长度分别为​m和​n，WDTW的时间复杂度与DTW的时间复杂度相同

改进的逻辑权重函数

如何根据两点之间的相位差系统地分配权重。在此提出修改后的逻辑权重函数（MLWF）。逻辑函数是仅使用一个方程的最流行的经典对称函数之一。然而，逻辑函数的标准形式在设置权重界限时并不灵活。因此，在本文中我们提出了改进的逻辑权重函数MLWF，它扩展了逻辑函数的性质。

在和加速度时序数据中，根据相位差确定的权重代表着什么信息？

在误判的时间序列中，可以理解为其中的重要时序波动与标准的摔倒时间序列中的时序波动的动态时间弯曲距离相近，所以导致神经网络将二者误判。那么如何将二者进行区分。根据惩罚权重让两个序列有更大的差异。

那么就是以加权动态时间弯曲距离作为目标函数，根据改进后的的逻辑权重函数给出路径中的相位差惩罚因子，根据惩罚因子小的位置加大差异。是的误判的时间序列与标准摔倒的时间序列有更大的差异，在插值给出差异之后，根据XX将插值点与邻近点进行结合，就是先插值，再根据插值改变原有的时间序列，使得二者的差异加大。通过神经网络对其训练来降低神经网络的误判率，提升识别精度。

权重值​w_{(i)}定义为：

公式（6）中​i=1,2,\cdots,m，​m是序列的长度，​m_c是序列的中点，​w_{max}是权重参数的期望上限，​g是控制函数曲率（斜率）的经验常数，也就是说通过​g控制相位差较大的点的惩罚水平。​g的取值范围为​[0,\infty)。

针对四种特殊情况研究了MLWF的特征。这四种情况的特点总结如下：

1. 恒权重（Constant weight）：这是对所有点赋予相同权重的情况。这可以在​g=0时实现。
2. 线性权重（Linear weight）：适用于权重与距离范围成线性比例的情况。这可以在​g=0.05时实现。那么​w_{(i)}的值几乎是线性增加的关系。
3. Sigmoid 权重（Sigmoid weight）：使用不同的​g值可以实现不同的sigmoid模式，例如当​g=0.25时，权重函数遵循sigmoid模式。
4. 两个不同的权重（Two distance weight）：在这种情况下，前半部分被赋予一个权重，而后半部分被赋予另一个权重。这可以在​g=3时实现

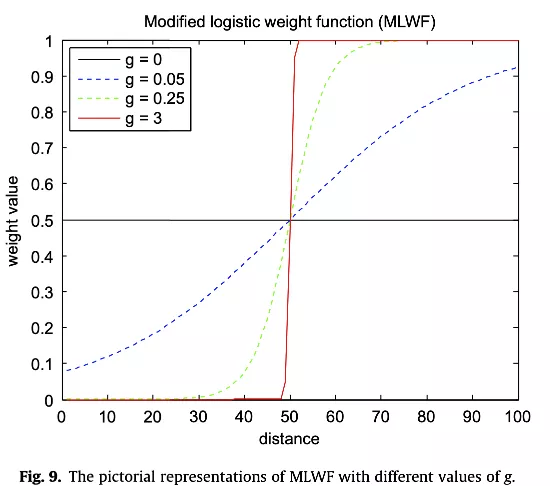
根据实证研究，最优​g的范围分布在​0.01\sim 0.6。更小的​g代表着对序列中更多的点的惩罚较少，因此WDTW的性能类似于DTW。

加权导数动态时间规整（WDDTW）

前面提出的加权概念可以扩展到DTW的变体，微分动态时间弯曲距离，也就是WDDTW（加权唯粉动态时间弯曲距离）。因为DTW可能会尝试通过扭曲X轴来解释Y轴的可变性，这可能会导致意外的 singularities ，即序列中的一个点与其它序列中的多个点之间的对应，以及其它不直观的对齐。为了克服DTW的这些缺点，DDTW将原始点转换为更高级别的特征，其中包含序列的形状信息。在序列​S中变换数据点​s_i的估计方程由下式给出：

其中​m表示序列​S的长度，因为没有定义第一个与最后一个估计值，所以在这里认为​d_1^s=d_2^s与​d_m^a = d_{m-1}^a

DDTW的加权版本如下：

其中​\xi^*(i,j) = |w_{|i-j|}(d_i^s-d_j^q)|^p+\min{\{\xi^*(i-1,j-1),\xi^*(i-1,j),\xi^*(i,j-1)\}}

​D_S与​D_Q分别为​S与​Q转换来的微分时间序列。