史密斯控制器 - Smith Predictor
原论文:《Smith Predictor Control and Internal Model Control - A Tutorial》
《Smith Predictor Control and Internal Model Control - A Tutorial》
Abstract (摘要)
本文旨在提供一种名为史密斯预估控制的时间延迟补偿方案指南。为了从新的理论概念理解史密斯预估控制,本文讨论了内部模型控制(IMIC)方案。还讨论了相关的主题,例如扰动抑制、H2最优性、稳定鲁棒性和饱和问题。
Keywords(关键词)
时滞系统,史密斯预测控制,内部模型控制
1. Introduction (引言)
时间延迟一直是控制系统闭环控制中需要克服的常见现象。近年来,控制应用的不断增加使得系统化地解决时间延迟问题变得更加重要。基于此观察,我们回顾了控制时间延迟系统的最著名方案之一。这种独特的方案是由O.J.M. Smith大约在50年前提出的,并且由于其实用性至今仍备受关注。从目前的观点来看,只要涉及时滞系统,内部模型控制(IMC)与Smith预测控制则密切相关。在分别介绍了两种控制方案的基本公式后,我们讨论了它们之间的等效性。基于等效性识别,我们讨论了相关主题。本文主要研究单输入单输出(SISO)系统,并针对MIMO系统中特有的问题讨论了多输入多输出(MIMO)系统。
2.Smith Predictor Control (史密斯预测控制)
Smith预测器控制是一种反馈控制方案,它包含一个如图1所示的副回路。G表示一个稳定的、严格真有理函数,它描述了被控对象的无延迟部分。L表示一个正常数、代表时间延迟。C和L分别是通过建模过程获得的G和L的标称版本。C_y表示一个有理函数,它描述了称为主控制器的补偿器。次级回路的作用是消除实际的延迟输出,并将预测输出反馈给主控制器。这使得在设计主控制器时可以假设控制回路中没有时间延迟。PID控制器可以与经典的整定技术一起成功应用。
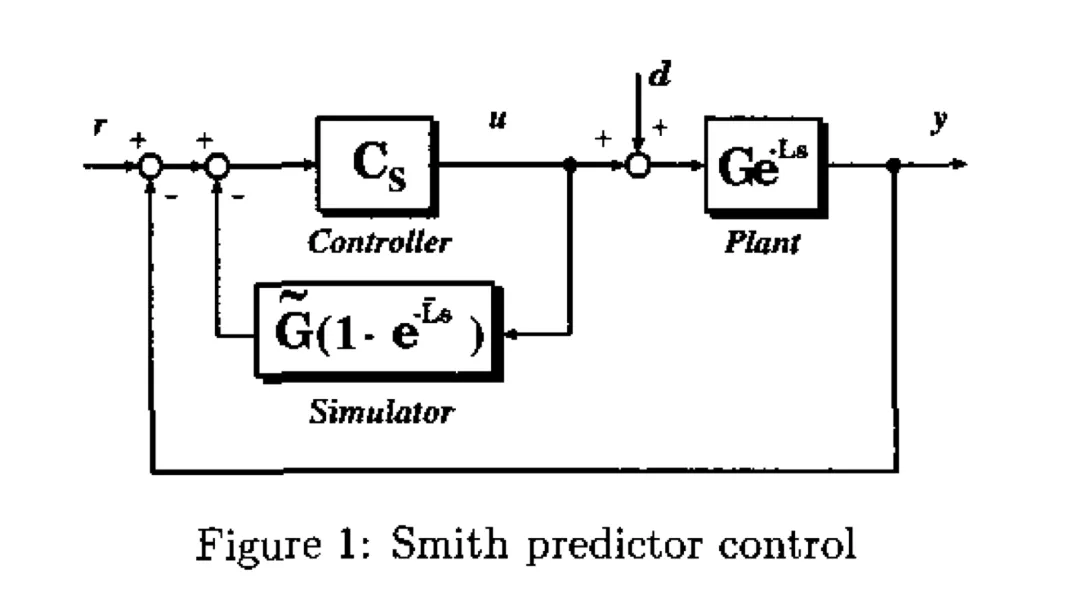
当G = \tilde{G}且L = \tilde{L}时,输出y依赖于参考输入r和扰动项d,如下:
由于分母函数1+GC_S是一个有理函数,因此闭环极点是有限个数。需要注意的是,对扰动的响应直接取决于G的极点,而G是不可控的,这个问题会在之后进行讨论。
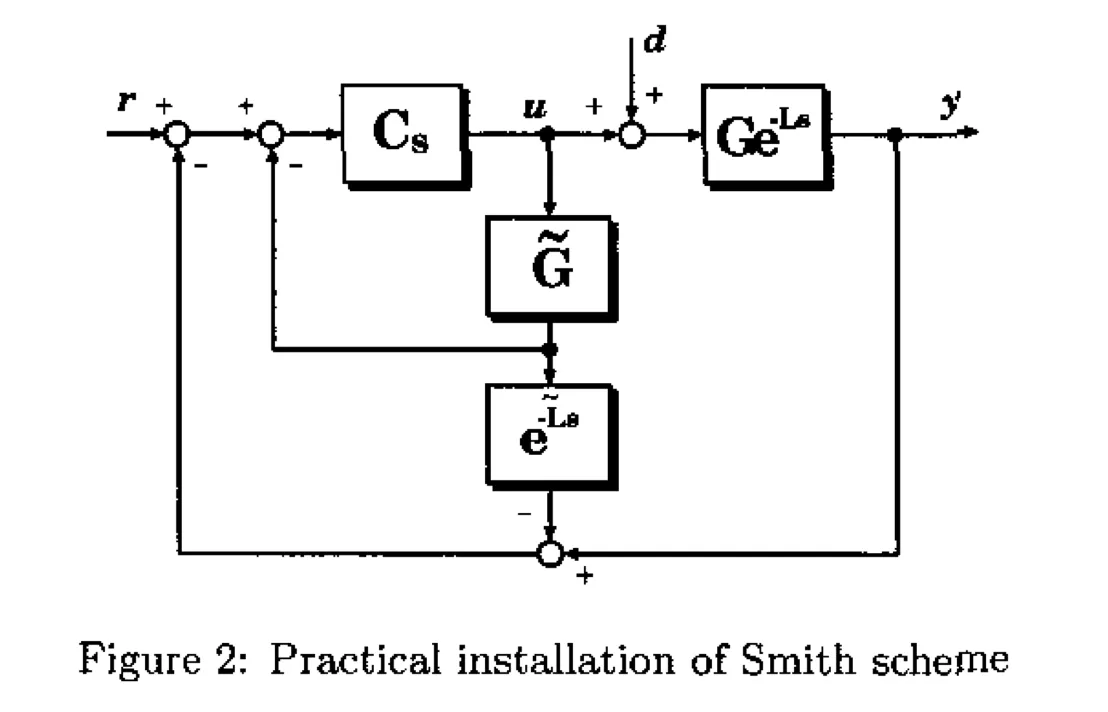
图2是Smith预测控制方案的另一个等效图,它可能更便于实际应用。
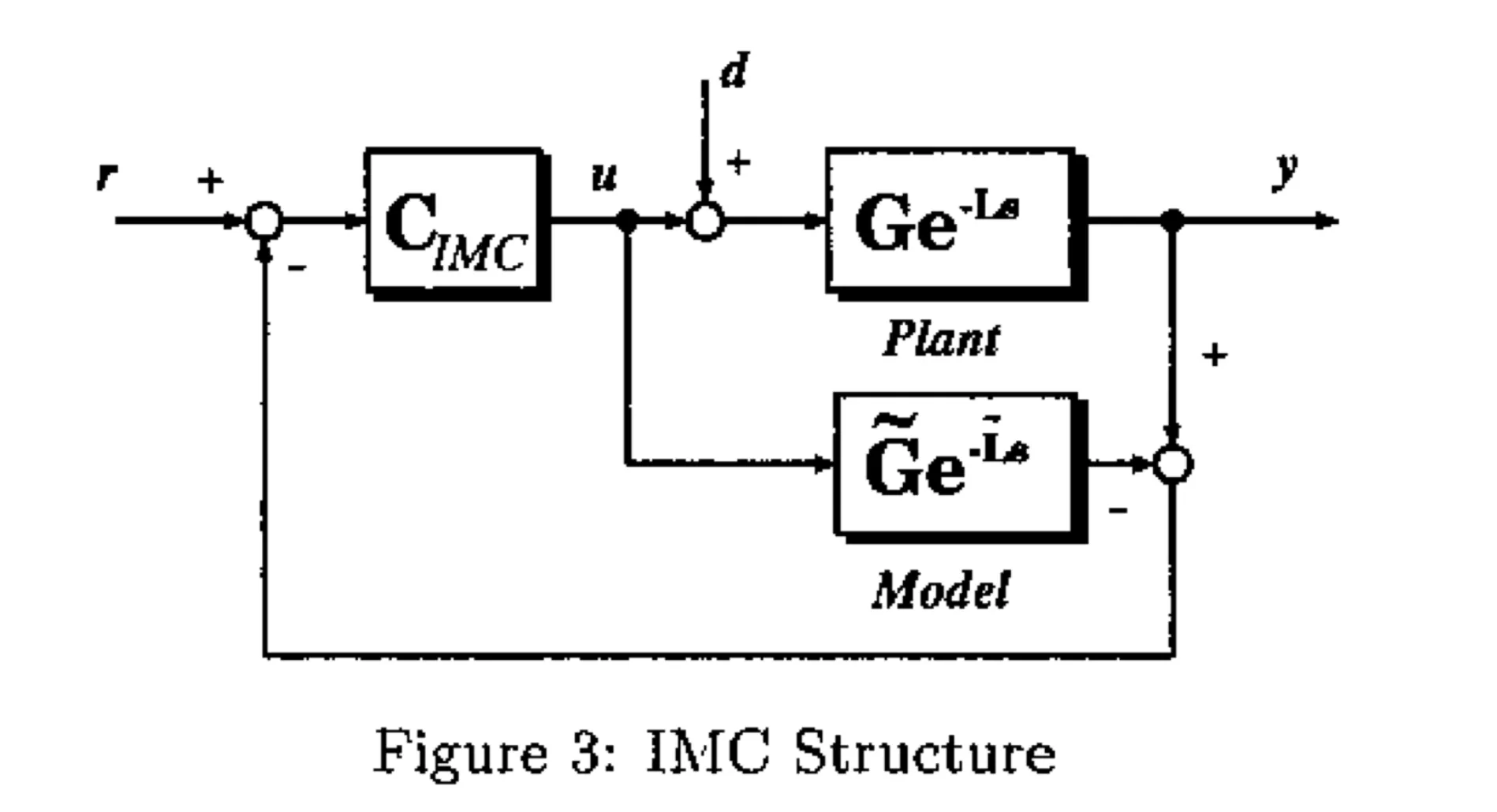
3. Internal Model Control(内部模型控制)
内部模型控制(IMC)是一种将工厂模型纳入控制的方案,如图3所示,G,L,\tilde{G}和\tilde{L}与第二节中提到的参数相同。C_{IMC}表示一个传递函数,它作为设计参数从稳定的有理函数中适当地选择。假设实际被控对象的动态行为与其模型完全一致,即满足\tilde{G}_e^{-\tilde{L}s} = G_e^{Ls},那么此时系统输出y与输入r之间将具有一种简单明确的关系,如下:
可以看出,只要使用稳定的参数C_{IMC}来控制稳定的系统,内不稳定性就能始终得到保证。
内部模型控制IMC的设计过程:
假设条件为G = \tilde{G},L = \tilde{L},且G为最小相移系统,此时IMC设计参数的一个简单选择是:
其中,F(s)是一个满足F(0) = 1的有理函数,称之为IMC滤波器,它的作用是保证所选择的C_{IMC}是一个严格正则的传递函数。
一个典型且简单的IMC滤波器F(s)的选择如下:
其中,\lambda是一个适当选择的正实数,n是一个适当选择的正整数。
由此得到的输入-输出关系表达式为:
需要特别注意的是,当滤波器F被选取为1时(即F(s) = 1),除去纯时延外可以实现完美的跟踪性能。
4. Equivalence(等价性)
将图1和图3的方框图进行比较,可以发现Smith方案和IMC方案有一个共同的特点,两者都利用被控对象模型来抵消对象自身的动态特性。基于图4的等效框图,我们可以找到一个将史密斯预测控制方案与IMC方案相互转换的公式,如下:
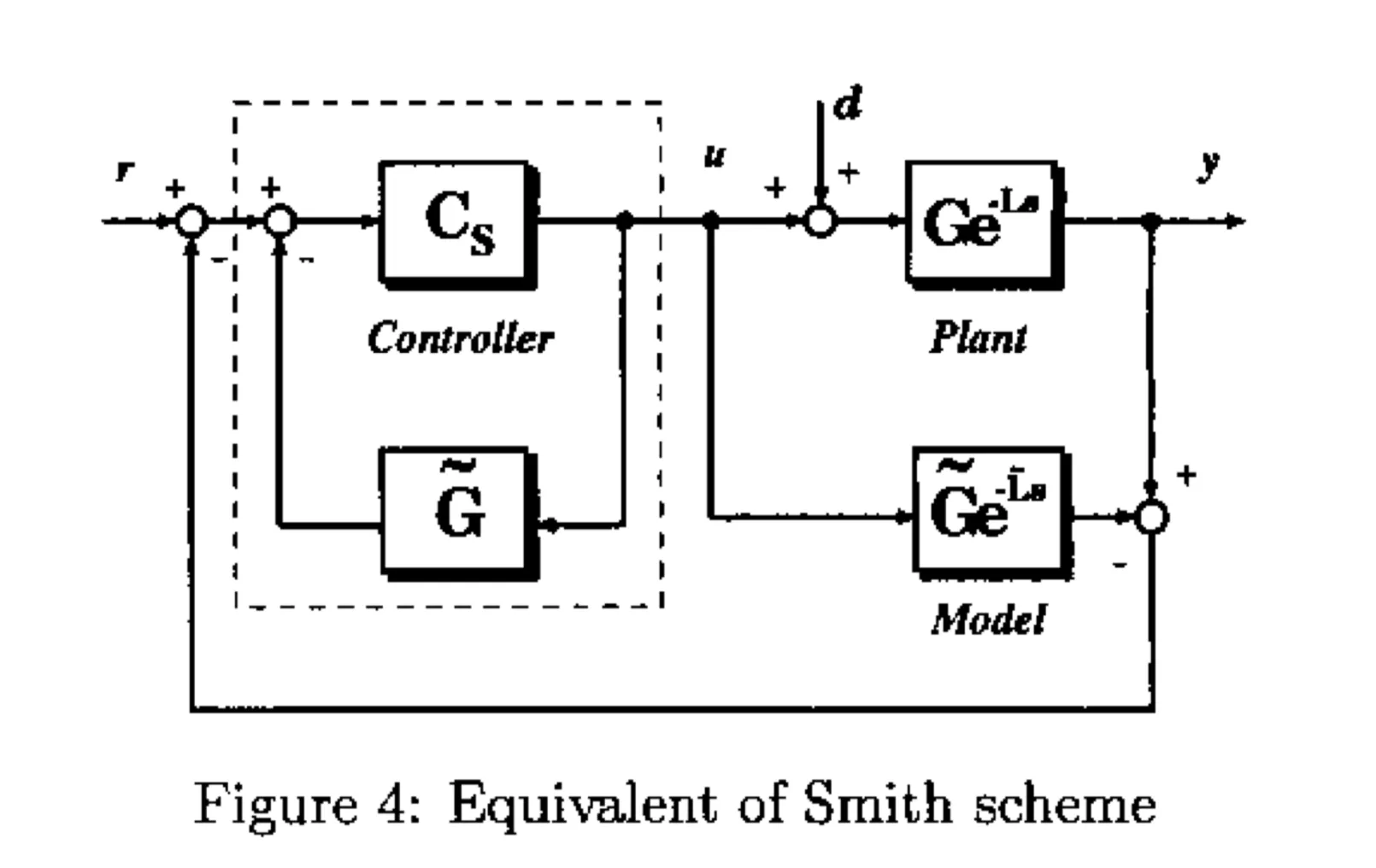
史密斯预测控制具有一种IMC(内部模型控制)的结构,其中IMC控制器C_{IMC}可通过主控制器进行参数化表示,并且这种设计方式与经典的单位反馈控制结构的设计方法类似。
对于原论文中的相关问题,缠绕问题及结论部分进行省略,具体可以查看原论文。
基于史密斯预估器的时滞系统控制研究- 摘录笔记
原论文:《基于史密斯预估器的时滞系统控制研究》
背景
现代工业生产过程往往伴随着时滞缓解,时滞环节会导致系统不能准确地跟踪系统的输入量。同时,当系统一旦产生外部扰动,系统的超调量会逐渐增加,影响系统的稳定性,通常情况下,当系统的滞后时间与时间常数比值大于0.5时,该系统则可以定义为大时滞系统,随着比值逐渐增加,整个系统的相位滞后也会随之增加,系统则会因为超调严重而出现故障,有些时候,甚至危及设备及人身安全。
因此,如何有效地补偿时滞环节成为了一个重要的课题,常见的时滞系统包括积分时滞系统(IPDT),一阶时滞系统(FOPDT),二阶时滞系统(SOPDT)以及一些非最小相位时滞系统等。发电厂中有很多水泵水箱的水位,比如,凝结水补水箱的水位,可以近似为一个积分时滞(IPDT)系统模型,而众多化工实验以及电气控制系统的模型一般都可以简化为FOPDT系统,造纸业的生产过程系统,由于其温度回路的阶跃响应曲线一般呈现为S型,对于这种动态过程具有明显的二阶特性,一般都采用SOPDT系统来进行描述。
为了解决时滞环节给系统带来的影响,Smith提出了传统的史密斯预估器,其工作原理是在系统的反馈回路中引入补偿装置,用来消除滞后因子对系统带来的影响,首先,需要对系统的动态特性进行估测,然后,通过预估补偿装置将滞后因子提前反映到系统的串联前向控制器,促使控制通道传递函数中的滞后因子与其他部分分离,从而消除滞后因子对系统的影响,在一定程度上加快系统的调节时间,使系统以最快的速度趋于稳定,消除系统的超调量,一般而言,时滞系统控制结构如下图所示。
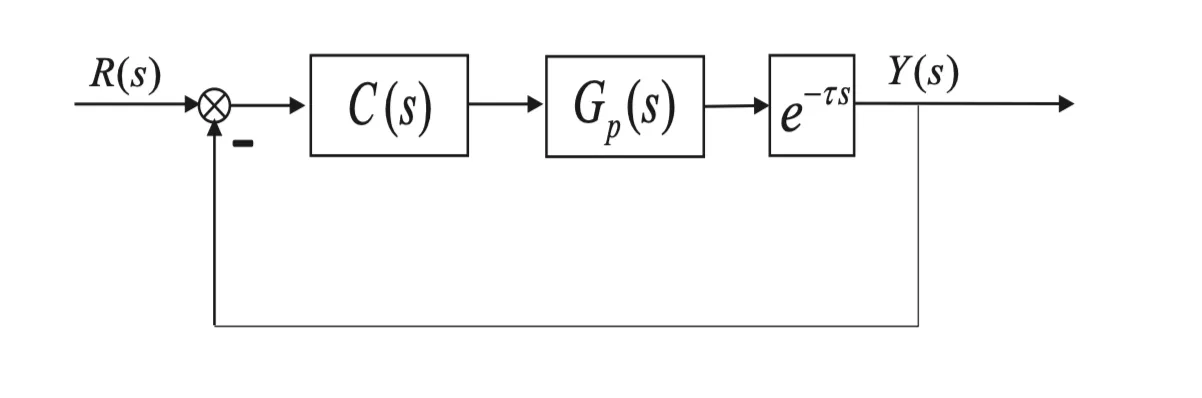
上图中,G(s) = G_p(s)e^{-\tau s}为系统的控制对象传递函数,G_p(s)是G(s)中不包含纯时滞特性部分的传递函数,C(s)为系统的前向控制器,史密斯预估器的原理便是在控制器C(s)两端并联一个补偿环节,用来补偿控制对象的时滞部分,这个补偿环节便是预估补偿器,预估器的传递函数一般记作G_m(s)(1-e^{-\tau_ms})因此,史密斯预估器的结构如下图所示。

上图中,G_p(s)为控制对象非时滞部分传递函数,\tau为控制对象时滞因子,G_m(s)为预估模型非时滞部分传递函数,\tau_m为预估模型时滞因子,通常情况下,G_p(s)\ne G_m(s),\tau\ne\tau_m,与此同时,C(s)为前向控制器,R(s)为系统的输入,Y(s)为系统的输出,Y_m(s)为系统的预估输出,系统的预估补偿器可以记作D(s),其传递函数为:
由上图可知系统的闭环传递函数为:
从而,由上式可以得到模型失配情况下闭环系统的特征方程为:
通常情况下,认为史密斯预估器中的控制对象和预估模型相互匹配,即G_p(s) = G_m(s),\tau = \tau_m时:
由此可知,对时滞系统闭环传递函数进行补偿后,系统的滞后因子e^{-\tau s}已经与其余部分相互隔离,其作用相当于如下图所示的系统等效图,该系统不会影响系统的稳定性,只是将输出滞后了一段时间。
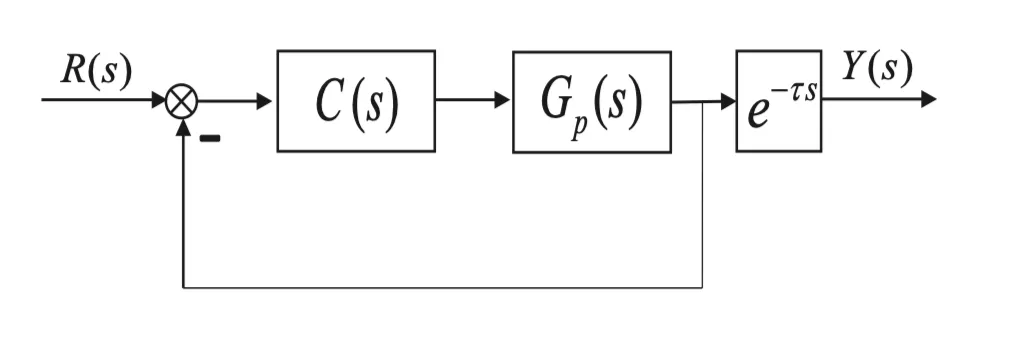
因此,由上式可知模型匹配情况下闭环系统的特征方程为:
由此可知,系统的特征方程中并不包含时滞因子,能够有效减小系统的超调量,从而提高系统的稳定性。
理解与示例
假设需要控制系统控制一个热水管道出口的水温,系统的特性如下:
-
调节阀门输入热水流量(控制信号u(t))来改变出口水温。
-
由于管道长度的存在,从阀门动作到出口温度变化,存在明显的纯滞后(此处假设热水管道的纯滞后为3分钟)。
-
假设延迟前的动态模型为一阶惯性模型,数学模型可表示为:
G(s) = \frac{2}{5s + 1} -
纯滞后的时延为L=3分钟。
因此,系统整体模型为:
其中,表达式中的变量s为拉普拉斯算子,e^{-Ls}为延迟项。
-
拉普拉斯变换是一种常用语控制理论和系统分析的数学工具,用于把复杂的微分方程转换为更简单的代数方程,便于分析。
-
变量s是复频域变量,定义为:s = \sigma + j\omega,其中\sigma为复频域的实部,表示系统衰减特性;\omega为复频域的虚部,表示系统的振荡特性。
-
在大多数简单的控制问题分析中,只需要将它看作一种数学记号即可,具体的,对于一阶惯性环节的拉普拉斯传递函数:
G(s) = \frac{K}{\tau s +1}其中,K表示增益,描述了输入变化一定量后输出的稳定变化量;\tau为系统时间常数,表示系统达到稳态的快慢特性;在上述的示例中,K=2,\tau=5所以简单建立出上述的数学模型。
因为直接使用传统控制方法时存在延迟3分钟的情况,那么就会导致:
- 控制器调整阀门后,出口温度并不会立即响应,控制器误以为动作无效而继续增加阀门开度。
- 当延迟过后,温度变化明显超出预期,导致系统超调、波动或振荡。
所以通过史密斯预估器进行时延问题的解决。
史密斯预测控制的过程如下:
step 1. 控制器做出控制动作
- 假设当前时间为t=10分钟。
- 假设控制器此刻开始调整热水阀门开度(输入信号u(10)),想要提高出口水温。
step 2. 模型即时输出(无延迟的预测输出)
- 内部非滞后模型G(s)立即对控制信号做出响应(注意,这只是内部预测模型计算的输出,并非真实输出)。
- 即时预测出口温度变化:G(s)u(10)。此时真实出口温度尚未变化。
step 3. 预测延迟后的输出(实际系统未来的输出)
- 内部预测模型继续记录3分钟前(t=7)的控制输入信号u(7),并计算此刻t=10的延迟预测输出,即G(s)u(7)。
- 这个输出表示预测系统在当前时刻的实际状态(3分钟前控制动作的真实效果)。
step 4. 形成预测误差(控制器实际使用的反馈)
- 此时,真实系统的实际出口水温传感器测量值也已经到达控制器,记为y_{real}(10)。
- 控制器内部则已经计算出了预测的延迟输出,记为y_{pre}(10) = G(s)u(7)。
- 预测误差为:e(10) = y_{real}(10) - y_{pre}(10)
- 如果预测完全准确,则e(10)\approx 0,控制器无需大幅调整动作。
- 如果实际输出和预测存在差异,比如因为扰动等原因,控制器根据这个误差调整控制动作,进行偏差修正。
step 5. 控制器依据预测误差调整控制信号
- 控制器利用上述预测误差信号e(t)做出适当调整动作。
- 如此循环,不断利用预测模型提前计算未来输出,并用预测误差信号来修正实时控制动作。
| 时间(分钟) | 控制输入 | 内部预测即时输出 | 延迟预测输出 | 实际输出(真实传感器) | 预测误差(反馈) |
|---|---|---|---|---|---|
| 7 | u(7) | G(s)u(7) | - | - | - |
| 8 | u(8) | G(s)u(8) | - | - | - |
| 9 | u(9) | G(s)u(9) | - | - | - |
| 10 | u(10) | G(s)u(10) | G(s)u(7)(7分钟动作的真实效果预测) | y_{real}(10) | y_{real}(10)-G(s)u(7) |
| 11 | u(11) | G(s)u(11) | G(s)u(8)(8分钟动作的真实效果预测) | y_{real}(11) | y_{real}(11)-G(s)u(8) |