无监督的数据异常检测算法（1）- LOF

#异常检测 #LOF
26

无监督的数据异常检测算法（1）- LOF

1.1 LOF简介

在众多的离群点检测方法中，LOF方法是一种典型的基于密度的高精度离群点检测方法。在LOF方法中，通过给每个数据点都分配一个依赖于邻域密度的离群因子LOF，进而判断该数据点是否为离群点。若LOF​\gg1，则该数据点为离群点；若LOF接近于1，则该数据点为正常数据点。

1.2 距离度量尺度

设对于没有相同点的样本集合​D，假设共有​n个检测样本，数据维数为​m，对于

\forall X_i = (x_{i1},x_{i2},\cdots,x_{im})\in R \qquad i=1,2,\cdots,n

针对数据集​D中的任意两个数据点​X_i,X_j，存在如下几种常用的距离度量方式：

  1. Euclid距离（欧几里得距离）
  2. Hamming距离（汉明距离）==汉明距离使用在数据传输差错控制编码里面，用于度量信息不相同的位数==
  3. Mahalanobis距离（马氏距离）
  4. 球面距离
  5. 除上述之外，还有切比雪夫距离，闵可夫斯基距离，绝对值距离，曼哈顿距离等，根据具体问题具体分析选择哪一种距离度量方式

在下述内容中统一使用​d(A,B)表示点​A和点​B之间的距离。根据定义，可以根据交换律得​d(A,B)=d(B,A)

1.3 LOF计算步骤

1.3.1 第​k距离

​d_k(O)为点​O的第​k距离，​d_k(O) = d(O,P)满足如下条件

  • 在集合中至少存在​k个点​P'\in D\{O\}使得​d(O,P')\le d(O,P)
  • 在集合中至多存在​k-1个点​P'\in D\{O\}使得​d(O,P')<d(O,P)

简而言之：点​P是距离​O最近的第​k个点

image-20221014142252520

确定的​k值在后续的离群点检测中十分重要，这个数值的确定表示在离群点的检测中通过带检测点周围多少个点来对其进行判断。

在确定了​k的值之后，也就是确定了第​k距离。因为有了第​k距离从而有了**​k距离邻域**

1.3.2 ​k距离邻域

设​N_k(O)为点​O的第​k距离邻域，满足：

N_k(O)=\{P'\in D\{O\}|d(O,P')\le d_k(O)\}

此处的邻域表示的是具体的点，这个邻域集合中包含所有到点​O的距离小于点​O第​k邻域距离的点。

同样由第​k距离得到的概念还有-可达距离

1.3.3 可达距离

以​O为中心，点​P到点​O的第​k可达距离定义为：

d_k(P,O)=\max{\{d_k(O),d(P,O)\}}

可达距离可以看作是一种简化，直接的衡量方式：

点​P到点​O的第​k可达距离至少是点​O的第​k距离。距离点​O最近的​k个点，他们到​O的可达距离被认为是相等的，都等于​d_k(O)

通过​k距离邻域和可达距离，引出了局部可达密度

1.3.4 局部可达密度

局部可达密度的定义为：

\rho_k(P) = \frac{1}{\sum_{O\in N_k(P)}\frac{d_k(P,O)}{|N_k(P)|}}=\frac{|N_k(P)|}{\sum_{O\in N_k(P)}d_k(P,O)}

局部可达密度表示点​P的第​k邻域内所有点到​P的平均可达距离。如果​P和周围邻域点是同一簇，那么可达距离更可能为较小的​d_k(O)，导致可达距离之和更小，局部可达密度更大。如果点​O和周围邻域点较远，那么可达距离可能会取较大值​d(O,P)，导致可达距离之和更大，局部可达密度更小。

通过局部可达密度引出了最终的LOF局部离群因子。

1.3.5 局部离群因子

LOF_k(P) = \frac{\sum_{O\in N_k(P)}\frac{\rho_k(O)}{\rho_k(P)}}{|N_k(P)|}

LOF局部离群因子则是点​P的邻域​N_k(P)内其他点的局部可达密度与点​P的局部可达密度之比的平均数。如果这个比值越接近于​1，说明点​O的邻域点密度差不多（相近），点​O的邻域点密度差不多，点​O则可能和邻域同属于一簇（不是离群点）；如果这个比值小于​1，则说明​O的密度高于其邻域点的密度，​O为局部的密集点（不是离群点）；如果这个比值大与​1，说明点​O的密度小于其邻域点密度，点​O可能是异常点。

根据局部可达密度的定义可以知道，如果一个数据点与其他点比较疏远的话，那么显然它的局部可达密度就会比较小。但是局部离群因子是通过一个数据点的局部可达密度与其​k距离邻域中的数据点的局部密度比较，获得一个相对的密度。这样就可以允许数据分布不均匀，密度不同。

1.4 示例

如下图所示：

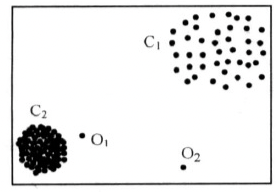
image-20221014173641385

图中是一个二维数据集，图中包含两个簇​C_1,C_2和两个离群点​O_1,O_2，其中​C_1更为稠密，​C_2稀疏，​O_1是局部离群点，​O_2是全局离群点。如果根据全局的异常因子检测方法，​O_2离群点易于挖掘，但是​O_1会难以挖掘。如果为了挖掘出​O_1而调整全局离群点检测的参数，那么​C_1中大部分的数据点都可能会被标识为离群点。